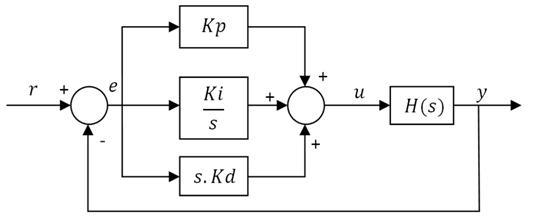
Rangkaian analog PID.
Kp adalah konstanta proporsional. Kp berlaku sebagai Gain (penguat) saja tanpa memberikan efek dinamik kepada kinerja kontroler. Ki adalah konstanta integral. Kontrol I dapat memperbaiki respon steady-state, namun pemilihan. Ki yang tidak tepat dapat menyebabkan respon transien (transient response) yang tinggi sehingga dapat menyebabkan ketidakstabilan system. Pemilihan Ki yang sangat tinggi justru dapat menyebabkan output berosilasi. Kd adalah konstanta derivatife dapat mengurangi efek overshoot (respon berlebihan) dalam menuju steady-state. Dengan kata lain, seolah-olah, control D mampu memprediksi error yang akan terjadi sebagai efek dari error yang dihitung sebelumnya.
Suatu sistem kontrol klasik kombinasi, baik PI ataupun PID, hanya dapat bekerja dengan baik untuk sistem H(s) yang cenderung linier dalam fungsi waktu. Artinya, persamaan dinamik dari model H(s) relatif tidak berubah selama rentang waktu pengontrolan. Padahal kenyataannya, tidak ada fenomena sistem riil yang benar-benar linier. Bahkan hampir semua fenomena kontrol mulai dari skala kecil misalnya kontrol motor DC, hingga skala sistem besar, misalnya kontrol pesawat terbang tanpa awak, jika dilakukan pemodelan secara rinci dan lengkap adalah sangat tidak linier (nonlinear). Setiap sistem riil selalu berhadapan dengan gangguan (disturbance). Motor selalu bermasalah dengan friksi pada poros, gearbox, perubahan karakteristik karena temperatur, dll. Pesawat di udara selalu berhadapan dengan tekanan udara yang berubah-ubah, angin, hujan, dsb.
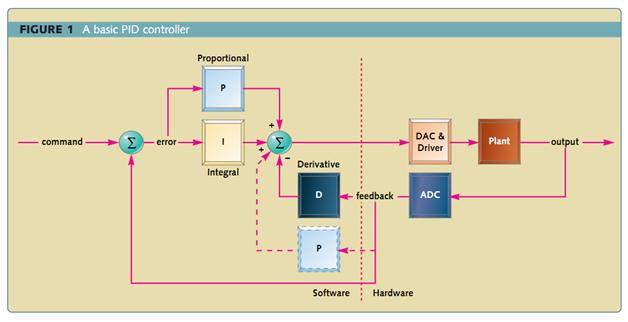
Figure 2-1 adalah schematic dari sebuah sistem dengan menggunakan kendali PID. Kendali PID membandingkan nilai yang terukur di y dengan nilai referensi yaitu nilai setpoint, y0. Nilai selisih atau error,e, kemudian akan digunakan untuk menghitung input proses yang baru, u. Input ini akan mencoba mengatur proses yang terukur agar kembali pada setpoint yang diinginkan.
Alternatif lain selain PID loop tertutup adalah PID loop terbuka. Kendali loop terbuka (tidak mempunyai umpan balik) dalam banyak kasus tidak memuaskan. Dengan menambahkan umpan balik dari output, performansi system dapat ditingkatkan.
Tidak seperti algoritma kendali sederhana, kendali PID dapat memanipulasi input dari proses berdasarkan keadaan sebelumnya dan tingkat perubahan sinyal. Hal ini member keakuratan dan metode kendali yang stabil.
Ide dasarnya adalah bahwa system kendali membaca keadaan system menggunakan sensor. Kemudian nilai pembacaan tersebut akan dipakai untuk mengurangi nilai referensi yang diinginkan untuk menghasilkan nilai error. Kemudian nilai error akan diolah menjadi tiga, untuk menangani keadaan sekarang, melalui persamaan proporsional, mencatat keadaan sebelumnya, untuk persamaan integral, dan untuk memprediksi keadaan setelah sekarang, melalui persamaan derivative.
Ideal Versus Standard PID
PID sering ditemukan dalam industry, dan yang paling mudah adalah bentuk standard. Dalam bentuk ini Kp digunakan pada persamaan I dan D.
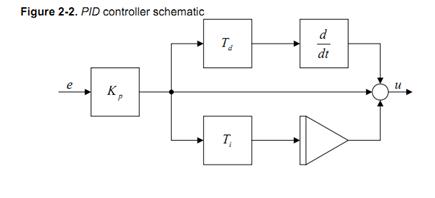
Figure 2-2 menunjukan schematic kendali PID, dimana Tp, Ti, dan Td menunjukan konstanta waktu dari proporsional, integral, dan derivative.
Td adalah waktu yang dibutuhkan untuk memprediksi keadaan selanjutnya. Komponen integral akan menyesuaikan dengan menjumlahkan semua nilai error sebelumnya dalam waktu Ti detik (atau sample).
Dalam bentuk idealnya adalah:
Dengan ini, jadi, Ki = Kp/Ti dan Kd=KpTd. Bentuk standar, meskipun sedikit lebih kompleks matematis, lebih digunakan pada industri.
Proporsional
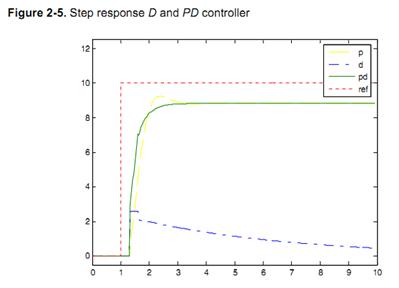
Persamaan proporsional (P) memberikan input proporsional untuk system kendali dengan error. Pada banyak kasus, dengan hanya menggunakan kendali P dapat memberikan nilai error yang tidak berubah (stationary error) kecuali ketika nilai input dari system kendali bernilai nol dan nilai proses sistem sama dengan nilai yang yang diinginkan. Pada Figure 2-3 stationary error dalam system muncul setelah adanya perubahan pada nilai yang diinginkan atau referensi (desired value). Nilai P yang besar akan mengakibatkan system tidak stabil.
Integral
Kendali integral (I) adalah penjumlahan dari error sebelumnya. Proses penjumlahan error akan berlangsung sampai nilai dari output system sama dengan nilai referensi yang diinginkan, dan hasil ini dalam keadaan stationary error ketika nilai referensi stabil. Penggunaan control I biasanya digabung dengan P yang disebut controlPI. Jika hanya menggunakan control I saja akan memberikan respon yang lambat dan seringkali mengakibatkan system berosilasi.
Derivatif
Control derivative adalah nilai dari tingkat perubahan error. Control ini akan meningkatkan respon system. Control D biasanya akan digunakan dengan control P atau PI sebagai kontrol PD atau PID. Pemberian D biasanya menyebabkan system tidak stabil. Respon dari control PD memberikan respon rising yang cepat daripada kontroler P. Pada dasarnya control D mempunyai sifat sebagai highpass filter pada sinyal error.
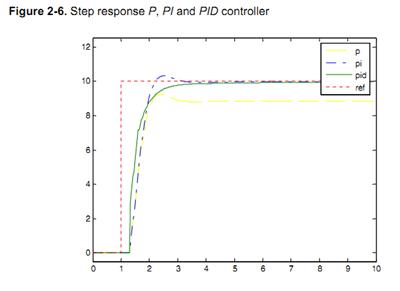
Dengan menggunakan ketiga control semuanya, sebagai kontroler PID biasanya memberikan performansi yang baik. Figure 2-6 memberikan perbandingan P, PI, dan PID. PI meningkatkan performansi P dengan menghilangkan stationary error, dan PID meningkatkan performansi PI dengan respon yang lebih cepat dan tidak ada overshoot.
Tuning
Manual Tuning
Set Kid an Kd menjadi nol. Kemudian tingkatkan nilai Kp perlahan sampai mencapai osilasi lalu set kembali sekitar menjadi setengahnya. Tikngkatkan Ki sampai mencapai hasil yang lebih baik. Akan tetapi, nilai Ki yang terlalu besar akan menyebabkan system tidak stabil. Terakhir, tingkatkan nilai Kd. Akan tetapi terlalu besar nilai Kd akan menyebabkan respon yang berlebihan dan overshoot.
Parameter-parameter Tuning
Cara yang paling baik untuk mencari nilai parameter-parameter PID yang cocok adalah melalui pemodelan matematika dari system yang akan dikontrol, parameter-parameter tersebut dapat dihitung untuk mendapatkan respon yang diinginkan. Tapi sering kali deskripsi yang detail secara matematis dari sebuah system kadang tidak tersedia, untuk itu tuning dilakukan dengan cara eksperimen (dicoba-coba sampai mendapat nilai yang cocok) terkadang dilakukan. Menemukan nilai PID itu sendiri merupakan sebuah pekerjaan yang menantang. Pengetahuan yang baik terhadap komponen-komponen yang bekerja pada system dan mengetahui cara-cara kendali lain adalah sebuah dasar yang baik. Beberapa proses terkadang mengharuskan tidak adanya overshoot dalam proses kendali terhadap setpoint. Secara umum, yang paling penting adalah kestabilan. Sebuah proses diharuskan tidak berosilasi untuk semua kondisi. Selanjutnya, harus dapat tercapai dalam jangka waktu tertentu.
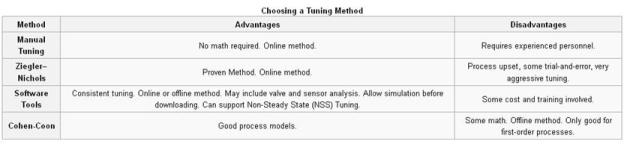
Ada beberapa metode untuk men-tuning PID. Pemilihan metode akan bergantung pada apakah proses bisa dituning secara online atau tidak. Metoda Ziegler-Nichols diketahui bersama sebagai sebuah cara untuk men-tuning secara online. Langkah pertama untuk men-tuning adalah mengatur konstanta gain I dan D menjadi nol, tingkatkan terus nilai penguatan P sampai terjadi osilasi yang stabil dan tanpa henti-hentinya (sebisa mungkin mendekati nilai yang diinginkan) pada output. Kemudian critical gain Kc(nilai Kp ketika system berosilasi terus-menerus secara teratur) dan perioda osilasi tersebut Pc sudah terekam dan nilai P, I dan D kemudian dapat ditentukan berdasarkan Table 2-1.
Selanjutnya, tuning parameter biasanya diperlukan untuk mengoptimasikan kinerja dari kontroler PID.
Harus digaris bawahi bahwa kontroler PID tidak akan bekerja dengan baik atau hanya akan bekerja pada area kecil sekitar system state tertentu. Terkadang bisa juga pada system non-linier, tetapi masalah umumnya datang pada kendali PID ketika system tidak stabil dan keadaan input tergantung pada keadaan system.
Kendali PID Diskrit
Sebuah kendali PID diskrit akan membaca error, menghitung dan memberikan putput terhadap input system pada waktu interval tertentu, pada perioda sampling T. Time sampling harus lebih kecil daripada konstanta waktu terkecil dari system.
Background Algoritma
Tidak seperti algoritma control sederhana, kendali PID dapat memanipulasi input system berdasarkan keadaan sebelumnya dan tingkat perubahan sinyal. Hal ini akan memberikan metode control yang lebih akurat dan stabil.
Figure 2-2 menunjukan schematic dari kontroler PID, dimana Tp, Ti, dan Td menyatakan konstanta waktu untuk proporsional, integral, dan derivative.
Fungsi alih berdasarkan system dari Figure 2-2:
Hubungan u dengan e dalam domain waktu adalah:
Pendekatan integral dan derivatife untuk mendapat bentuk diskret, menggunakan:
Dimana n adalah waktu diskret pada waktu t.
Sehingga persamaan dari kontroler:
Dimana:
Jika input control tidak berubah terhadap waktu, maka:
Implementasi
:Contoh fungsi PID:
:File lainnya:
Permasalahan pada Integral
Biasanya nilai integral akan menjadi cukup tinggi ketika terjadi perbedaan yang mencolok antara PV(process value) dan SP(setpoint value) dikarenakan pada system terdapat beban(load) yang besar melebihi kemampuan system. Jika dalam kontroler menggunakan integral, hal ini bisa jadi masalah. Nilai dari konstanta integral akan terus bertambah, dan ketika beban yang besar dihilangkan, maka PID akan menghasilkan nilai selisih yang besar sampai konstanta integral kembali normal.
Hal ini dapat dicegah menggunakan beberapa cara. Dengan membatasi nilai konstanta integral agar tidak melewati nilai dari MAX_I_TERM. Nilai dari MAX_I_TERM tergantung pada system dan waktu sampling yang digunakan.
>> share :








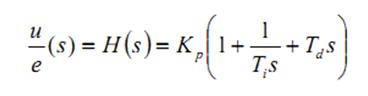

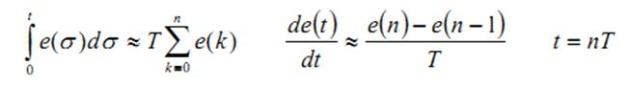

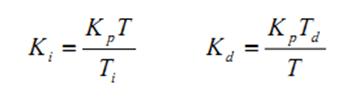

Belum ada tanggapan untuk "Mengenal Kendali PID"
Posting Komentar